1. Проекція з тривимірного простору на площину [ правити | правити код ]
2. Проекція з довільного простору на його підпростір [ правити | правити код ]
3. Ортогональна проекція на пряму і на напрям [ правити | правити код ]
4. Неортогональної проекція на пряму і на напрям [ правити | правити код ]

Цей термін має також інші значення див. проекція .

проекція ( лат. projectio - «викидання вперед»)

1. зображення тривимірної фігури на так званій картинної (проекційної) площині способом, що представляє собою геометричну ідеалізацію оптичних механізмів зору , фотографії , камери-обскури . Термін проекція в цьому контексті також означає метод побудови такого зображення і технічні прийоми, в основі яких лежить цей метод. Широко застосовується в інженерної графіки , архітектурі , живопису і картографії . Вивченням методів побудови проекцій як інженерна дисципліна займається Нарисна геометрія .
2. узагальнення проекції в першому сенсі (точніше - її різновиди - паралельної проекції) для відображення точок, фігур, векторів простору будь-якої розмірності на його підпростір будь-якої розмірності, наприклад, крім проекції точок тривимірного простору на площину, це може бути проекція точок тривимірного простору на пряму, точок площини на пряму, точок 7-мірного простору на його 4-мірне підпростір і т. п., а також проекція вектора на будь-який підпростір вихідного простору, і в особливості, як особливо важливий АСТН випадок, на пряму або на напрямок. Проекція в цьому сенсі знаходить широке застосування в відношенні векторів (як в елементарному контексті, так і в абстрактному), при використанні декартових координат і т.п.

відображення P: A → A {\ displaystyle P \ colon A \ to A} з простору в себе називається проекцією, якщо P ∘ P = P {\ displaystyle P \ circ P = P} , Тобто при повторному застосуванні відображення результат не змінюється: P (P (a)) = P (a) ∀ a ∈ A {\ displaystyle P (P (a)) = P (a) \ quad \ forall a \ in A } .

Проекція з тривимірного простору на площину [ правити | правити код ]

Проекційний метод зображення предметів заснований на їхньому зоровому поданні. Якщо з'єднати всі крапки предмета прямими лініями (проекційними променями) з постійною точкою О (центр проекції), в якій передбачається очей спостерігача, то на перетині цих променів з будь-якої площиною виходить проекція всіх точок предмета. Таким чином отримуємо на площині перспективне зображення предмета або центральну проекцію.

Якщо центр проекції нескінченно віддалений від картинної площини, то говорять про паралельну проекції; при цьому, якщо проекційні промені падають перпендикулярно до площини - то про ортогональної проекції, а якщо похило - про косокутній проекції.

Якщо площину проекції не паралельна жодної з координатних площин - це аксонометрична проекція .

• При будь-якому вигляді проекції відрізок прямої переходить у відрізок прямої (в виродженим випадку - коли відрізок лежить на проекційному промені - в точку); пряма може перейти в пряму або в промінь.
• Це властивість помітно спрощує додаток проекції в образотворчих цілях, особливо в технічному кресленні, коли об'єкт містить багато прямолінійних елементів. В останньому випадку досить спроектувати кінці відрізків і з'єднати їх на кресленні прямими.
• Еліпс або окружність переходять в еліпс (в виродженим випадку - в відрізок або окружність).

Проекція з довільного простору на його підпростір [ правити | правити код ]

Проекція в цьому сенсі (згадана у вступі в пункті 2) - широко застосовується в лінійної алгебри (Докладніше, див .: Проекція (лінійна алгебра) ), Але на практиці не тільки в досить абстрактних контекстах, а й при роботі з векторами будь-якої природи, розмірності і ступеня абстракції, і навіть в елементарній геометрії, а також - дуже широко - при використанні прямолінійних координат (як прямокутних або афінних ).

Окремо слід згадати проекцію точки на пряму і проекцію вектора на пряму (на напрям).

Ортогональна проекція на пряму і на напрям [ правити | правити код ]

Найчастіше використовується ортогональна проекція.

Термін проекція в цьому сенсі вживається і щодо самої операції проектування, і щодо її результату (при операції проектування на пряму образи точки, вектора, безлічі точок називаються проекцією точки, вектора, безлічі точок на цю пряму).

Елементарне опис ортогональної проекції точки на пряму зводиться до того, що з точки на пряму слід опустити перпендикуляр, і його перетин з прямою дасть образ точки (проекцію точки на цю пряму). Це визначення працює і на площині, і в тривимірному просторі, і в просторі будь-якої розмірності.

Елементарне визначення проекції вектора на пряму найлегше дати, представивши вектор спрямованим відрізком. Тоді на пряму можна спроектувати його початок і його кінець, і спрямований відрізок від проекції початку до проекції кінця вихідного вектора дасть його проекцію на пряму.

Проекцією вектора на деякий напрямок зазвичай називають число, що збігається за абсолютною величиною з довжиною проекції цього вектора на пряму, визначальну цей напрямок; знак ж числа вибирається так, що воно вважається позитивним, коли напрямок цієї проекції збігається з даним напрямком, і негативним, коли напрям протилежний.

Неортогональної проекція на пряму і на напрям [ правити | правити код ]

Неортогональної проекція використовується рідше, до того ж навіть при використанні, особливо в елементарних контекстах, цей термін не завжди використовується.

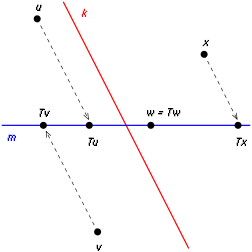
Перетворення T є косокутній проекцією уздовж k на пряму m. U = m і V = k

Найпростіше неортогональної проекцію на пряму можна задати, задавши саму цю пряму і площину (в двовимірному випадку - замість площині іншу пряму, в разі n мірного простору - гіперплоскость розмірності (n -1)), що перетинає пряму. Проекція точки визначається як перетин площині (гиперплоскости), що містить цю точку і паралельна площині, яка задає проекцію.

У разі, коли площину (гіперплоскость), що задає проекцію, ортогональна прямий, ми отримуємо ортогональную проекцію (це може бути її альтернативним визначенням). Тому власне для неортогональної проекції треба вимагати, щоб ця ортогональность була відсутня.

Для неортогональної проекції вектора на пряму і на напрям визначення виходять, виходячи з наведеного визначення проекції точки, прямо аналогічно тому, як це було описано в параграфі про ортогональної проекції.

• Треба, правда, мати на увазі, що за замовчуванням під проекцією вектора на пряму або на напрям розуміється все ж ортогональна проекція.

Проте поняття неортогональної проектування може бути корисним (по крайней мере, якщо не боятися термінологічної плутанини) для введення косокутних координат і роботи з ними (через них може бути в принципі досить легко визначено поняття координат точки і координат вектора в цьому випадку).